IDA*算法
-
IDA是对迭代加深搜索IDDFS的优化,我们可以把IDA看作A*算法思想在迭代加深搜索中的应用。
-
IDDFS仍然是一种“盲目”的搜索方法,只是把搜索范围约束到了可行的空间内。如果在进行IDDFS的时候能预测当前DFS的状态,不在继续深入下去,那么我们就可以节约很大部分的时间,不在搜索这个分支,从而提高程序效率。
-
同之前的A*的算法,这个预测就是在IDDFS中增加一个估价函数。在某个状态,经过函数计算,发现后续搜索无解,就返回。简单地说,就是在IDDFS的过程中利用估价函数进行剪枝操作,我们看一道例题:
【例题】破坏正方形
题解
-
首先要处理出每个正方形的所有边编号
-
这也就是这题的难点,考虑如何描述一个正方形
-
我们可以用三个值描述一个正方形:
-
正方形边长和左上角横、纵坐标
-
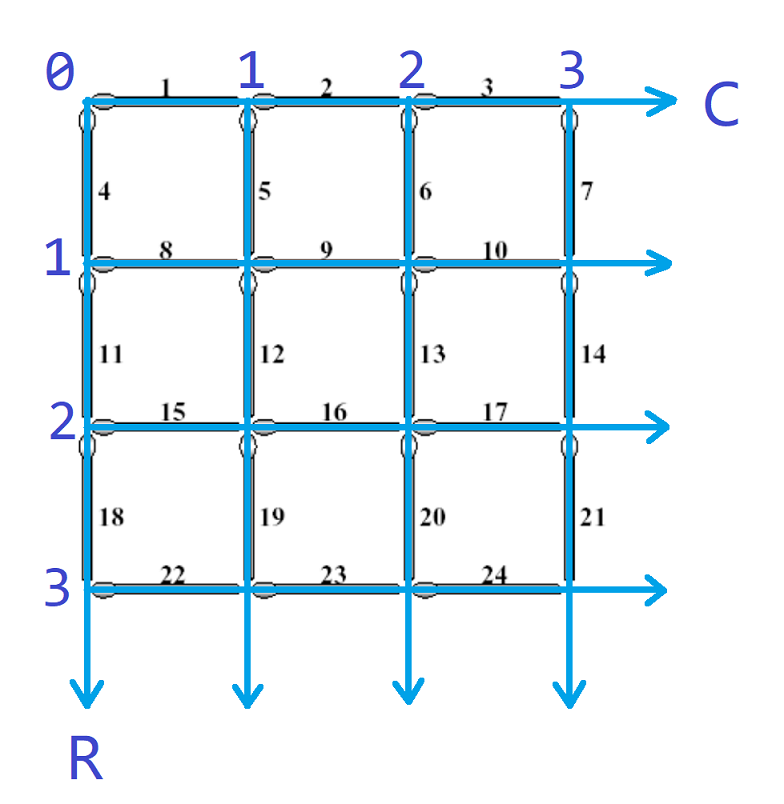
那么我们接下来要做的就是对于每组 正方形边长和左上角横、纵坐标,找出它所有边的编号。
-
对于所有横着的火柴,我们将其坐标定义为其左端点坐标
-
对于所有竖着的火柴,我们将其坐标定义为其上端点坐标
-
举个例子,编号为15和18的火柴的坐标都是(2,0)
-
先考虑横着的火柴。对于坐标为(r,c)的火柴,其编号即为 坐标为 (r, 0) 的火柴的编号+c。而所有坐标为(r,0)的火柴的编号,正好构成一个 首项为1,公差为2n+1 的等差数列,其中 n 为网格边长。那么坐标为(r,0)的火柴,编号为1+r(2n+1)。所以坐标为(r,c)的火柴,编号为1+r(2n+1)+c。
-
再考虑竖着的火柴。对于所有坐标为(r,c)的火柴,其编号为 与其坐标相同的横着的火柴的编号+n所以坐标为(r,c)的火柴,编号为1+r(2n+1)+c+n
-
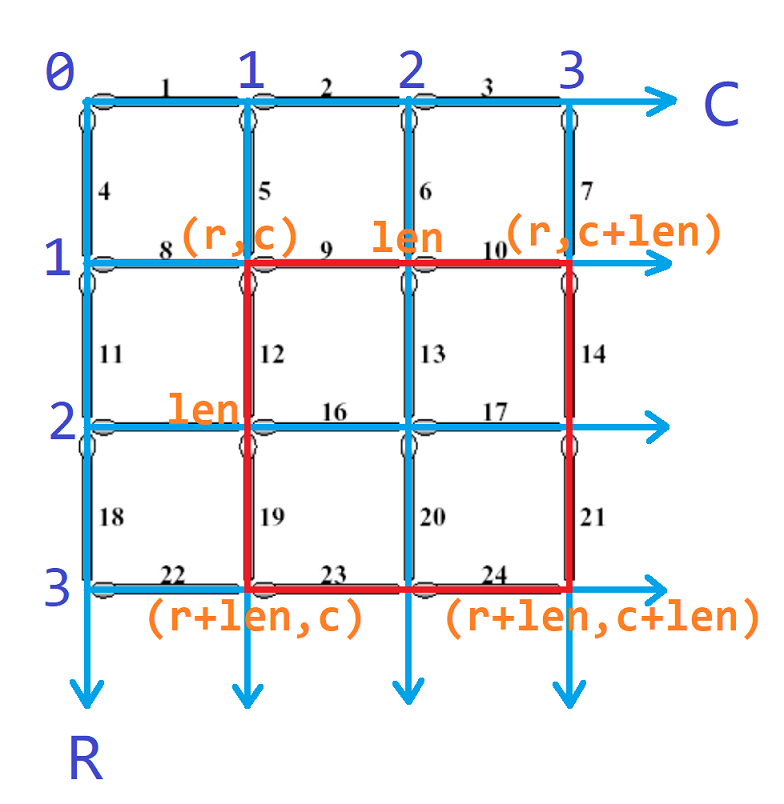
然后考虑每个正方形所包含的所有火柴的横纵坐标。对于一个左上角坐标为(r,c),边长为len的正方形,不难发现其四个顶点的坐标分别为(r,c),(r+len,c),(r,c+len),(r+len,c+len)。
-
考虑横着的火柴(以下i都从0开始),对于上边从左往右第 i个火柴,其坐标为(r,c+i),所以其编号为 1+r(2n+1)+c+i。对于下边从左往右第 i个火柴,其坐标为(r+len,c+i),所以其编号为 1+(r+len)(2n+1)+c+i。考虑竖着的火柴,对于左边从上往下第 i个火柴,其坐标为(r+i,c),所以其编号为 1+(r+i)(2n+1)+c+n。对于右边从上往下第i个火柴,其坐标为(r+i,c+len),所以其编号为 1+(r+i)(2n+1)+c+len+n。所以我们只需要从0到 len 枚举i,然后加边即可。
-
然后问题变成最少选出多少边,使得每个正方形中至少被选出一条边。
-
这是一个经典的重复覆盖问题,可以用 Dancing Links 求解。
-
这里我们不适用DLX这个数据结构,直接求解。
估计函数:
枚举所有未被删掉的正方形,将其所有边全部删掉,只记删除一条边。这样估计出的值一定不大于真实值,满足IDA*对估价函数的要求。其实这也是Dancing Links求解重复覆盖问题时的估价函数。
搜索顺序优化:
找出最小的未被删除的正方形,依次枚举删除每条边。
时间复杂度
搜索空间是指数级别的,但由于启发函数和剪枝的存在,实际搜索到的状态较少。
//DC Songxingan
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
const int N = 61; // 网格最大是 5 * 5 的,其中最多会有 5 * (5 + 1) * 2 = 60 个正方形,所以要开到 61
int n, idx; // n 为网格规模,idx 为正方形数量
int max_depth; // IDA* 的 max_depth
vector<int> square[N]; // 存每个正方形边上的火柴的编号
bool used[N]; // 存每个火柴是否已经被破坏
// 新加一个左上角坐标为 (r, c),边长为 len 的正方形
void add(int r, int c, int len)
{
int d = n << 1 | 1;
// 由于用到的 2n + 1 比较多,这里先用一个变量代替掉 2n + 1
vector<int> &s = square[idx];
s.clear(); // 有多组测试数据,需要上一组数据的内容清空
for (int i = 0; i < len; i++)
{
s.push_back(1 + r * d + c + i); // 上边第 i 个
s.push_back(1 + (r + len) * d + c + i); // 下边第 i 个
s.push_back(1 + n + r * d + c + i * d); // 左边第 i 个
s.push_back(1 + n + r * d + c + i * d + len); // 右边第 i 个
}
idx++;
}
// 判断正方形 s 是否完整
bool check(vector<int> &s)
{
for (int i = 0; i < s.size(); i++)
if (used[s[i]])
return false; // 如果其中有一条边已经被破坏了,那么说明不完整
return true; // 如果每条边都没被破坏,说明完整
}
// 估价函数
int f()
{
static bool backup[N];
// 由于要改动 used,需要先新建一个备份数组
memcpy(backup, used, sizeof used); // 将 used 复制到备份数组中
int res = 0;
for (int i = 0; i < idx; i++) // 枚举所有正方形
if (check(square[i])) // 如果某个正方形是完整的,
{
res++; // 那么 res ++ ,并将该正方形所有的边都删去
for (int j = 0; j < square[i].size(); j++)
used[square[i][j]] = true;
}
memcpy(used, backup, sizeof used); // 复制回来
return res;
}
// IDA*
bool dfs(int depth)
{
if (depth + f() > max_depth)
return false;
for (int i = 0; i < idx; i++) // 枚举所有的正方形
if (check(square[i])) // 如果第 i 个正方形还没被破坏
{
// 那么枚举该正方形的所有边编号,去掉该边并继续爆搜
for (int j = 0; j < square[i].size(); j++)
{
used[square[i][j]] = true;
if (dfs(depth + 1))
return true;
used[square[i][j]] = false;
}
// 如果每条边都爆搜不成功,那么说明删掉 max_depth 个火柴无法破坏该正方形
return false;
}
return true; // 如果所有的正方形都被破坏了,返回 true
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
scanf("%d", &n), idx = 0; // 初始化 idx
memset(used, false, sizeof used); // 初始化 used
for (int len = 1; len <= n; len++)
// 枚举 len, r, c,预处理每个正方形
for (int r = 0; r + len <= n; r++)
for (int c = 0; c + len <= n; c++)
add(r, c, len);
int k;
scanf("%d", &k);
while (k--) // 读入所有已经被破坏的边
{
int x;
scanf("%d", &x);
used[x] = true;
}
max_depth = 0; // IDA*
while (!dfs(0))
max_depth++;
printf("%d\n", max_depth);
}
return 0;
}
